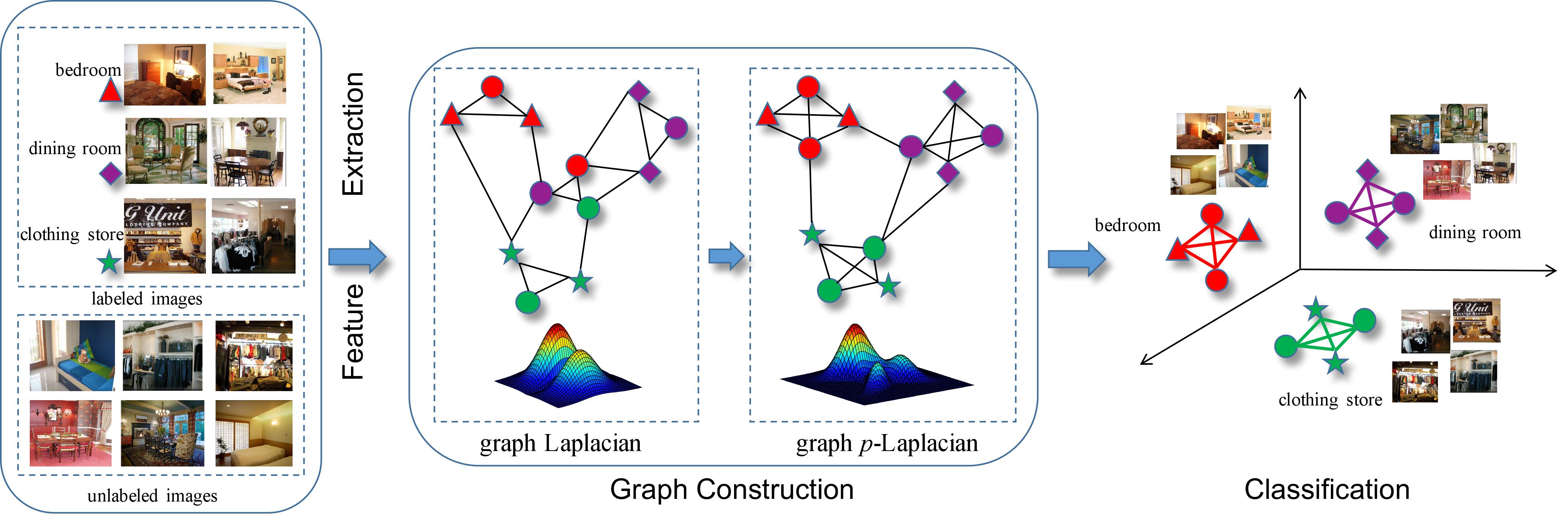
p-Laplacian Regularization for Scene recognition
Weifeng Liu, Senior Member, IEEE, Xueqi Ma, Yicong Zhou, Senior Member, IEEE, Dapeng Tao, and Jun Cheng, IEEE Transactions on Cybernetics, IEEE [PDF]

In this paper, we introduce a fully efficient approximation algorithm of graph p-Laplacian, which significantly saving the computing cost. And we propose p Laplacian Regularization (pLapR) to preserve the local geometry.

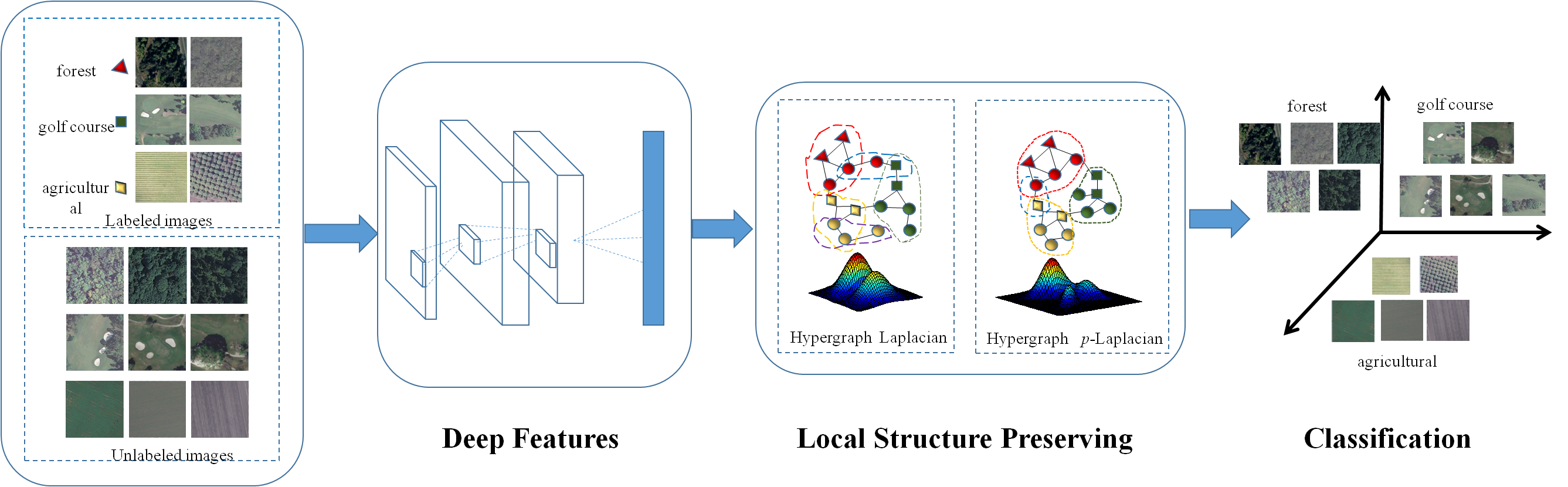
Hypergraph p-Laplacian Regularization for Remotely Sensed Image Recognition
Xueqi Ma, Weifeng Liu, Senior Member, IEEE, Shuying Li, Dapeng Tao, and Yicong Zhou, Senior Member, IEEE, IEEE Transactions on Geoscience and Remote Sensing, IEEE [PDF]

In this paper, we present an efficient and effective approximation algorithm of Hypergraph p-Laplacian and then propose Hypergraph p-Laplacian regularization (HpLapR) to preserve the geometry of the probability distribution. In particular, Hypergraph is a generalization of a standard graph while Hypergraph p-Laplacian is a nonlinear generalization of the standard graph Laplacian. The proposed HpLapR shows great potential to exploit the local structures.

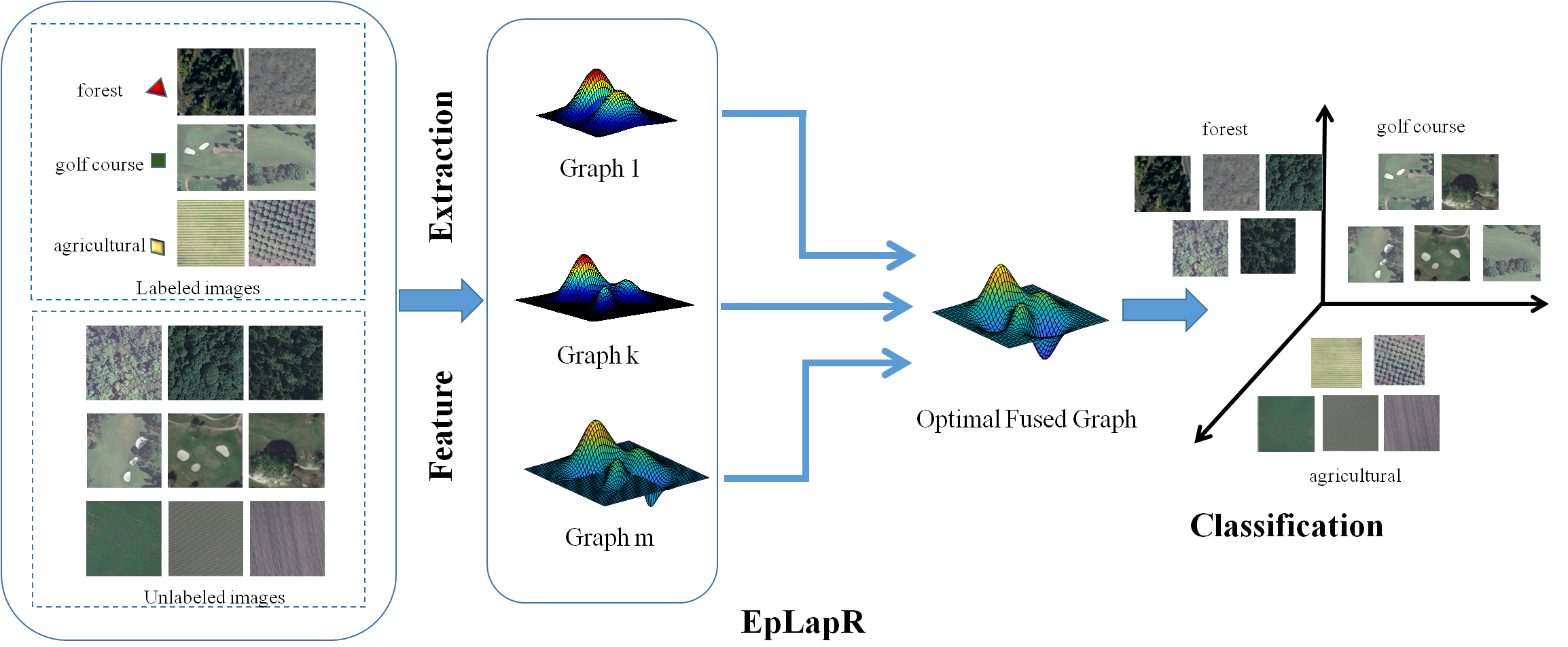
Ensemble p-Laplacian Regularization for Remote Sensing Image Recognition
Xueqi Ma, Weifeng Liu, Dapeng Tao, and Yicong Zhou, Cognitive Computation, Under Review [arXiv]

As a natural nonlinear generalization of graph Laplacian, p-Laplacian has been proved having the rich theoretical foundations to better preserve the local structure. However, it is difficult to determine the fitting graph p-Lapalcian i.e. the parameter p which is a critical factor for the performance of graph p-Laplacian. Therefore, we develop an ensemble p-Laplacian regularization (EpLapR) to fully approximate the intrinsic manifold of the data distribution. EpLapR incorporates multiple graphs into a regularization term in order to sufficiently explore the complementation of graph p-Laplacian. Specifically, we construct a fused graph by introducing an optimization approach to assign suitable weights on different p-value graphs. And then, we conduct semi-supervised learning framework on the fused graph. Extensive experiments on UC-Merced data set demonstrate the effectiveness and efficiency of the proposed method.

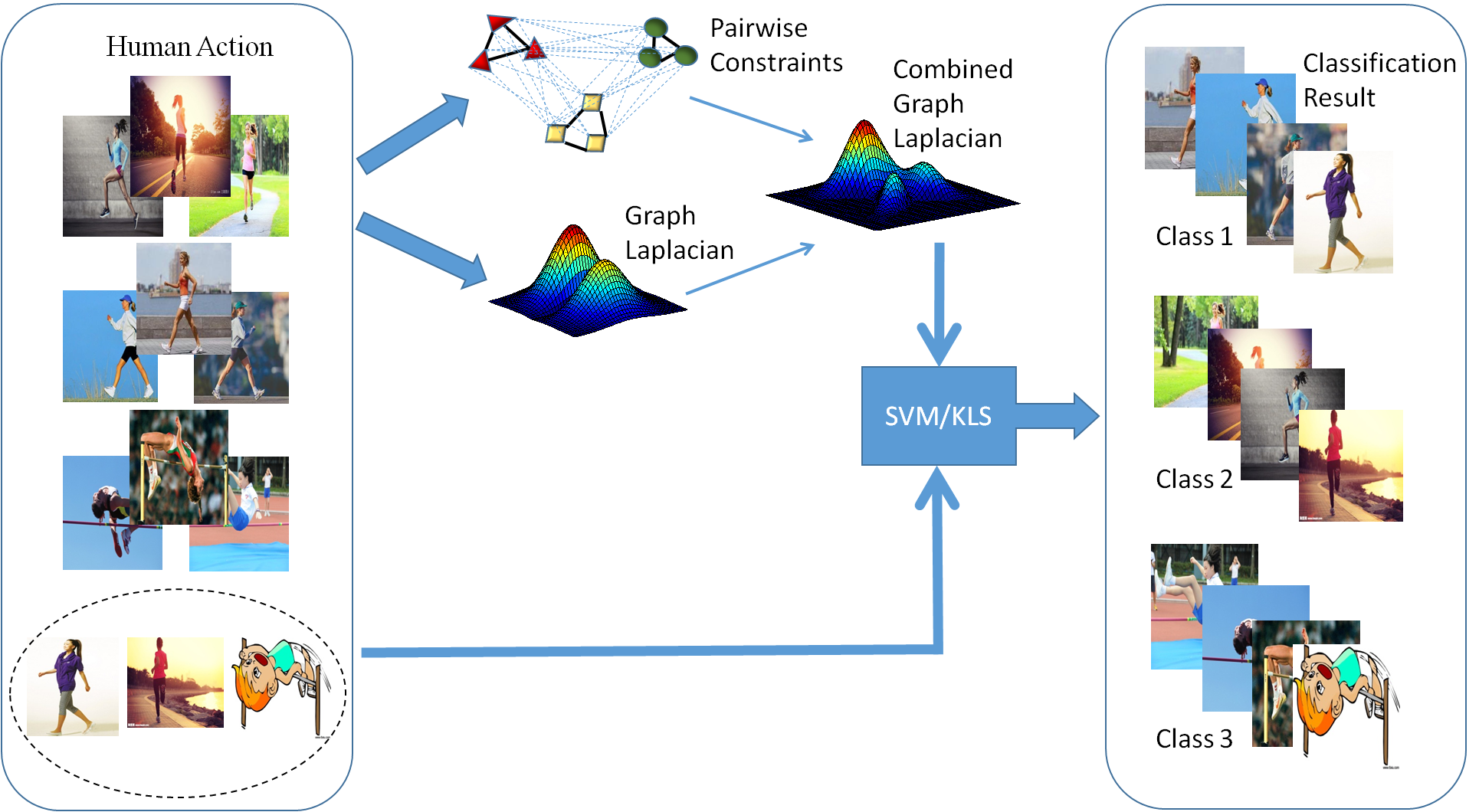
Effective human action recognition by combining manifold regularization and pairwise constraints
Xueqi Ma, Dapeng Tao, and Weifeng Liu, Multimedia Tools and Applications [PDF]

In this paper, we introduce a novel local structure preserving approach by considering both manifold regularization and pairwise constraints. Specifically, we construct a new graph Laplacian that takes advantage of pairwise constraints compared with the traditional Laplacian. The proposed graph Laplacian can better preserve the local geometry of data distribution and achieve the effective recognition. Upon this, we build the graph regularized classifiers including support vector machines and kernel least squares as special cases for action recognition.

Local Structure Preserving Using Manifold Regularization and Pairwise Constraints for Action Recognition
Xueqi Ma, Zhengyang cao, Weifeng Liu, Senior Member, IEEE, 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, 2016, pp. 480-486.

In this paper, we propose a local structure preserving method that effectively integrates manifold regularization and pairwise constraints. Particularly, we construct a new graph Laplacian by combining the traditional Laplacian and pairwise constraints. The new graph Laplacian can better preserve the local geometry and then further boost the performance.

Semi-supervised Hessian Eigenmap for Human Action Recognition
Xueqi Ma, Jiaxing Pan, Yue Wang, Weifeng Liu, Senior Member, IEEE. Intelligent Visual Surveillance, Springer Singapore, 2016.

In this paper, we integrate exact mapping information of certain data points into Hessian Eigenmap and propose semi-supervised Hessian Eigenmap. Considering the prior information with physical meaning, semi-supervised Hessian Eigenmap can approximate global low dimensional coordinates. On the other hand, Hessian can exploit high-order information of the local geometry of data distribution in comparison with graph Laplacian and thus further boost the performance.

Multiview p-Laplacian Regularization for Image Recognition
Xueqi Ma, Weifeng Liu, Senior Member, IEEE, Shuying Li, Dapeng Tao, and Yicong Zhou, Senior Member, IEEE , IEEE Transactions on Cybernetics, Under Review

As a nonlinear generalization of graph Laplacian, graph p-Laplacian provides convincing theoretical evidence to better preserve the local structure. In addition, images usually have different representations, such as color, shape, and texture. So, we present multiview -Laplacian regularization (mpLapR) to obtain the complete representation of the local geometry of the data distribution.

Manifold Regularization
Xueqi Ma and Weifeng Liu, Intechopen, Accepted

In this chapter, we first present some related work of manifold learning, and then introduce several extensions based on the manifold regularization framework.

High order local structure preserving algorithms based on p-Laplacian regularization

Principle Investigator

Develop local structure preserving algorithms with p-Laplacian regularization, Hypergraph p-Laplacian regularization, Ensemble p-Laplacian regularization and Multiview p-Laplacian regularization.

Cloud album

Principle Investigator

An app can storage a large amount of photos.

Image annotation based on multiview depth sparse coding and Manifold Regularization

Project Member

Developed image processing algorithms combining multiview depth sparse coding with manifold regularization.

Summer School-Ecole Polytechnique and University of La Rochelle

Project of Data Science for Document Analysis Understanding.

To be responsible for all the affairs of the class

Honors: "Excellent graduate class", "Excellent undergraduate class"

President of the social and Eloquence Association

Voluntary High School Teacher